Pour exposer correctement la question de manière à la fois pédagogique et ludique, le plus simple est de visionner cette excellente vidéo qui dure une dizaine de minutes : cliquez ici pour voir la vidéo. Vous aurez compris qu’il s’agit de l’écart d’un facteur 10122 entre deux valeurs d’énergie du vide : celle, théorique, de l’énergie du vide quantique et celle, observée, issue du modèle cosmologique standard i.e. la constante cosmologique Λ.
English version published in open access : A simple mathematical solution to the cosmological constant problem.
Avec : mp pour masse de Planck, lp pour longueur de Planck , « h barre » constante de Planck réduite , c vitesse de la lumière dans le vide, Λ constante cosmologique. Enfin, A/C qui est la valeur habituelle de la catastrophe du vide soit environ 10122. On note que A/C=C/B donc C2=A*B.
Deux compléments en bas de l’image permettent de comprendre le pourquoi des astérisques.
– soit la densité volumique d’énergie du vide en mécanique quantique en J/m^3 :
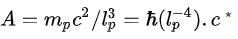
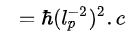

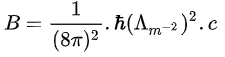
– La densité volumique d’énergie de la constante cosmologique C est la moyenne géométrique de A et de B :

autrement dit, la formule classique de la densité volumique d’énergie de la constante cosmologique.
avec ces deux compléments pour simplifier la vérification :
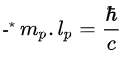
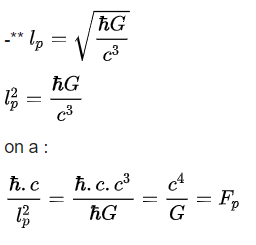
Méthode utilisée :
- On écrit la densité volumique du vide de la mécanique quantique, A, avec la constante réduite de Planck pour faire apparaitre une unité de dimension L-2
- On suppose une densité volumique du vide de la constante cosmologique en mécanique quantique, B, toujours avec la constante réduite de Planck, sur le même modèle dimensionnel que A . [ la constante cosmologique de dimension L-2 est de même dimension que lp–2 ].
- On démontre que la densité volumique du vide de la constante cosmologique de la relativité générale, C, est la moyenne géométrique de A et B
pour une confirmation de la méthodologie : cliquer sur ce lien pour voir l’article
Vous trouverez ici la formule de la densité volumique d’énergie de la constante cosmologique.
Vous trouverez ici la confirmation que lp-2= 3.83 1069m-2 est la valeur de l’énergie du vide en théorie quantique des champs.
On peut critiquer cette solution car elle n’est que mathématique et ne donne pas de sens physique contrairement à d’autres solutions. Néanmoins elle est beaucoup plus abordable d’un point de vue mathématique.
____________________________________________
édition du 15/01/2020
Je viens de remarquer que ce rapport :
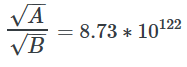
est la valeur exacte de la catastrophe du vide dans cette approche du problème.
On a donc deux racines carrées de densité volumique d’énergie, celle de A et celle de B, dont la multiplication donne la valeur de la densité volumique d’énergie de la constante cosmologique ( C en J/m3), et le rapport donne la valeur de la catastrophe du vide. En plus d’une simple solution mathématique au problème de la constante cosmologique, il semble qu’il y ait là une légère progression dans la compréhension de la question et l’esquisse d’une piste à suivre pour dénouer le problème.
La question qui se pose désormais est : quel est le sens physique de la racine carrée d’une densité volumique d’énergie (de A ou de B) ? Il n’existe pas de référence sur Wikipédia sur ce sujet pour la cosmologie. Il y en a une pour la « densité d’énergie cohésive » sur la version anglaise : cf Paramètre de solubilité d’Hildebrand.
____________________________________________
édition du 16/06/2022
Bien sûr parler de solubilité de vide de la QFT dans le vide de la constante cosmologique « quantique » est un non sens physique. En revanche, en relevant que la valeur de la densité d’énergie du vide de la QFT est exactement celle de la densité d’énergie de la masse de Planck (mPl c2/lPl3), la solubilité de cette dernière dans le vide de la constante cosmologique « quantique » fait sens physique.
____________________________________________
édition du 19/02/2022
Essai d’interprétation de cette solution mathématique avec l’effet Casimir
Nous avons,
– densité volumique d’énergie du vide en mécanique quantique A:
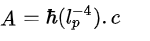
– l’hypothétique densité volumique d’énergie du vide de la constante cosmologique en mécanique quantique, B :
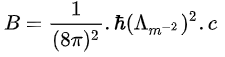
– densité volumique d’énergie de la constante cosmologique C est la moyenne géométrique de A et de B :
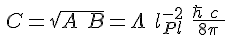
ce qui est exactement la formule (1) vue ici. Cette formule pourrait alors s’interpréter comme un effet Casimir mêlant énergie du point zéro du vide et l’hypothétique densité volumique d’énergie du vide de la constante cosmologique en mécanique quantique. Dans ce cas, cela validerait l’hypothétique densité d’énergie du vide de la constante cosmologique en mécanique quantique.
English version published in open access : dimensional complement of the mathematical solution to the cosmological constant problem.
Retrouvez la chronologie de la publication des articles à partir de la Présentation du blog