article remanié le 6 octobre 2021 et édité le 10 février 2022
Bonjour. N’ayant pu trouver une interprétation physique à ma solution mathématique du problème de la constante cosmologique, j’ai regardé vers d’autres voies.
Notez bien que ce qui va suivre dans cet article est spéculatif et comporte plus que probablement des approximations voire des erreurs. Néanmoins il me parait intéressant de signaler cette proposition.
Ayant lu « les particules d’un gaz parfait ont des vitesses proches de celles de la lumière » et sachant que la formule de la constante cosmologique peut être interprétée comme l’expression d’un fluide parfait à pression négative au fil de mes recherches sur les moteurs de recherches j’ai trouvé la notion de coefficient de traînée .
Sa définition et sa dimension m’ont parues suffisamment intéressantes pour faire une vérification numérique avec les données / formules retenues que j’utilise ou propose :
Définition du coefficient de traînée :
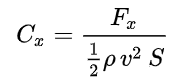 adimensionné.
adimensionné.
avec
![]() a la valeur de c, vitesse de la lumière car la constante cosmologique se comporte comme un gaz parfait ….
a la valeur de c, vitesse de la lumière car la constante cosmologique se comporte comme un gaz parfait ….
![]() = Force de Planck (édit : = c4/G )
= Force de Planck (édit : = c4/G )
![]() longueur de Planck au carré, soit la surface de Planck, plus petite surface que l’on connaisse en physique
longueur de Planck au carré, soit la surface de Planck, plus petite surface que l’on connaisse en physique
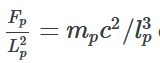 densité d’énergie de Planck en J/m3
densité d’énergie de Planck en J/m3
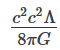 = Masse volumique de Λ * c2 = densité d’énergie de la constante cosmologique en J/m3
= Masse volumique de Λ * c2 = densité d’énergie de la constante cosmologique en J/m3
avec ![]() on a :
on a :
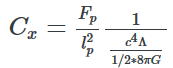
soit la moitié de la valeur du problème de la constante cosmologique en unités de Planck car ![]()
édit du 10 février 2022
Il semble que l’on puisse interpréter la valeur du problème de la constante cosmologique comme un coefficient de traînée d’une surface de Planck résistant au « fluide de la constante cosmologique » ? (à la vitesse c ?, vitesse de la lumière ) .
Pour cette ébauche d’interprétation j’ai utilisé ce document : Traînée subie par les corps en mouvement .
édition le 27 octobre 2020
On pourra relever que, tout au long de ce blog, je ne fais pas appel à l’énergie du vide de la mécanique quantique des champs (QFT) pour la formulation du problème de la constante cosmologique.
édition du 27 mars 2021
De plus, il est possible de trouver la valeur de l’énergie du point zéro de la QFT dans un cadre déterministe. J’ai été très longtemps dans le doute sur cette question en raison de la rareté de la documentation gratuite en ligne sur cette valeur.
Finalement, il y a quelques semaines j’ai réussi à mettre la main sur cette valeur dans cet article soit 3,83 1069 m-2. Il n’est pas surprenant de constater qu’il s’agit ni plus ni moins de la valeur en unités de Planck mise à la dimension adéquate. Dit clairement il s’agit simplement de lp-2 . Pourquoi faire simple quand on peut faire compliqué ?
Retrouvez la chronologie de la publication des articles à partir de la Présentation du blog