J’ai trouvé utile de faire un article de synthèse sur ma solution du problème de la constante cosmologique et de son lien avec l’effet Casimir. J’espère que cela vous permettra un abord plus aisé que par la lecture des deux articles qui y sont déjà consacrés et leurs multiples éditions. Bonne lecture.
mp masse de Planck, lp longueur de Planck , tp temps de Planck,
ħ constante de Planck réduite,
c vitesse de la lumière dans le vide,
Λ constante cosmologique.
A densité volumique d’énergie du point zéro en mécanique quantique.
B la densité volumique d’énergie de la constante cosmologique Λ en mécanique quantique.
C = ρΛ c2 densité volumique d’énergie de la constante cosmologique.
Enfin A/C qui est la valeur habituelle de la catastrophe du vide soit environ 10122. On note que A/C=C/B donc C2=A*B.
I. Résolution de la catastrophe du vide :
– définissons A, la densité volumique d’énergie du point zéro en mécanique quantique (J/m3) :
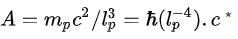
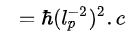
avec ce complément pour vérifier :
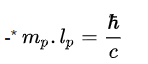
en effet lp-2 =3,83 1069 m-2 est la valeur de l’énergie du vide dans la théorie quantique des champs.
– définissons B, la densité volumique d’énergie de la constante cosmologique Λ en mécanique quantique. C’est là que la l’exposé diffère de la présentation classique de la catastrophe du vide.
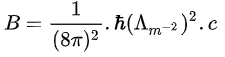
Méthode utilisée :
- On écrit la densité volumique du vide en mécanique quantique, A, avec la constante réduite de Planck pour faire apparaître une unité de dimension [L-2].
- On suppose une densité volumique du vide de la constante cosmologique en mécanique quantique, B, toujours avec la constante réduite de Planck, sur le même modèle dimensionnel que A . [ la constante cosmologique de dimension L-2 est de même dimension que lp–2 ].
Pour rappel, voici une présentation classique du problème de la constante cosmologique, i.e de la catastrophe du vide :
A / C =8 π lp-2 / Λ
A / C = 8,7 10122 , nombre sans dimension.
– La densité volumique d’énergie de la constante cosmologique C en cosmologie relativiste est la de moyenne géométrique A et de B :
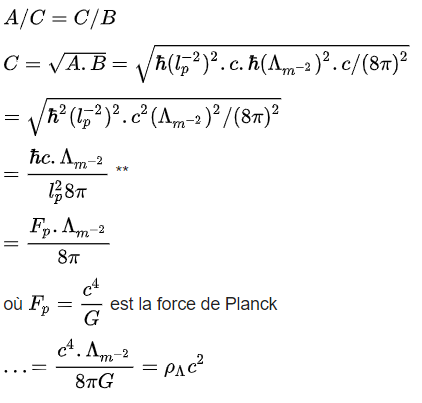
autrement dit, la formule classique de la densité volumique d’énergie de la constante cosmologique.
Avec ce complément pour faciliter la démonstration :
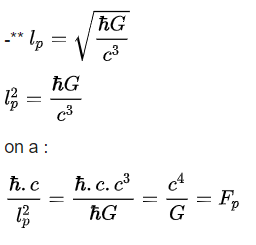
Méthode utilisée suite et fin :
- On démontre que la densité volumique du vide de la constante cosmologique de la relativité générale dans le modèle cosmologique standard, C, est la moyenne géométrique de A et B.
pour une confirmation de la méthodologie : cliquer sur ce lien pour voir l’article
On notera que l’on peut retrouver la valeur de la catastrophe du vide en mécanique quantique cosmologique de la même manière qu’en cosmologie relativiste avec :
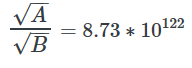
La question qui peut se poser est : quel est le sens physique de la racine carrée d’une densité volumique d’énergie (de A ou de B) ? Il n’existe pas de référence sur Wikipédia sur ce sujet pour la cosmologie. Il y en a une pour la « densité d’énergie cohésive » sur la version anglaise : c f Paramètre de solubilité d’Hildebrand.
Bien sûr parler de solubilité de vide de la QFT dans le vide de la constante cosmologique « quantique » est un non sens physique. En revanche, en relevant que la valeur de la densité d’énergie du vide de la QFT est exactement celle de la densité d’énergie de la masse de Planck (mPl c2/lPl3), la solubilité de cette dernière dans le vide de la constante cosmologique « quantique » fait sens physique.
English version published in open access : A simple mathematical solution to the cosmological constant problem.
II. Lien entre l’effet Casimir et la constante cosmologique :
On a vu en dans le paragraphe I. :
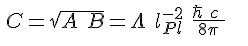

C, densité d’énergie de la constante cosmologique Λ, correspond à l‘égalité (1), autre écriture de la densité d’énergie de la constante cosmologique
Du point de vue de l’interprétation, il n’existe pas de « plaques physiques » susceptibles de jouer un rôle des surfaces en cosmologie pour l’effet Casimir . En revanche il parait acceptable de supposer que 1/dS = Λ joue le rôle de l’énergie de dimension [L-2] , auquel il faut en plus diviser par 8pi en cosmologie relativiste, ou, en théorie quantique des champs (1/dS = 1/lp2).
Ce changement de « rôle » serait comparable à celui que l’on a opéré avec la constante cosmologique Λ, initialement prévue pour rendre compte d’un univers statique pour finalement , en changeant de coté dans l’équation, rendre compte de l’accélération de l’expansion de l’univers.
On aurait ainsi une validation théorique de ce nouvel effet Casimir en mécanique quantique cosmologique et, par conséquent, une validation de la définition de B comme densité d’énergie de la constante cosmologique Λ en mécanique quantique.
Avec lp-2 = 3.83 1069 m-2, énergie du vide ( =énergie du point zéro) dans la théorie quantique des champs
Retrouvez la chronologie de la publication des articles à partir de la Présentation du blog